Basic Usage
Introduction
Most tasks can be completed using the exact_extract function.
The following examples demonstrate the use of exact_extract to summarize population and elevation data from the Gridded Population of the World and EU-DEM datasets.
The exactextractr R package package includes samples of both of these datasets, cropped to the extent of São Miguel, the largest and most populous island of the Azores archipelago. The package also provides boundaries for the six municipalities, or concelhos, that cover the island. These files can be accessed from GitHub.
Loading the sample data
The exact_extract function can accept inputs from several popular libraries such as GDAL, rasterio, fiona, and GeoPandas. A filename can also be provided, in which case exact_extract will load the data using whichever of these libraries is available.
Although it is not needed to complete the analysis, the following code can be used to plot the sample datasets.
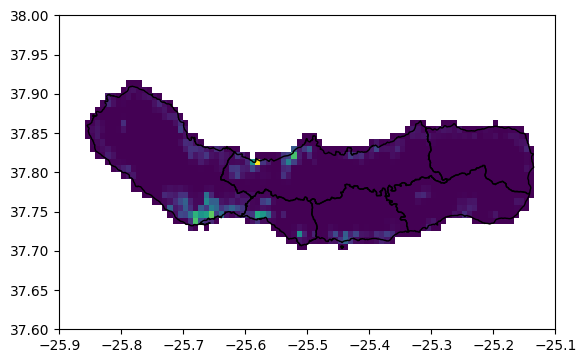
The plot below shows the population count file from GPW. This raster provides the total population in each pixel for the calendar year 2020. On top of the population grid, we plot boundaries for the six municipalities, or concelhos, into which the island is divided. We can see that the population is concentrated along the coastlines, with smaller communities located in volcanic calderas inland.
[1]:
import exactextract
import geopandas as gpd
import rasterio
import rasterio.plot
from matplotlib import pyplot
pop_count = 'sao_miguel/gpw_v411_2020_count_2020.tif'
concelhos = 'sao_miguel/concelhos.gpkg'
fig, ax = pyplot.subplots()
with rasterio.open(pop_count) as r:
rasterio.plot.show(r, ax=ax)
admin = gpd.read_file(concelhos)
admin.plot(ax=ax, facecolor='none', edgecolor='black')
[1]:
<Axes: >
Calculating the total population
Because the population count raster has been cropped and contains no land area outside of São Miguel, we can calculate the total population of the island by simply loading the raster into a NumPy array and using the sum function:
[2]:
with rasterio.open(pop_count) as r:
r.read(masked=True).sum()
Calculating the population per region
We can use the exact_extract function to see how the population is divided among concelhos. By default, the results are returned in a GeoJSON-like format, with the order corresponding to the order of input features.
[3]:
from exactextract import exact_extract
exact_extract(pop_count, concelhos, 'sum')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/3334375047.py", line 3, in <module>
exact_extract(pop_count, concelhos, 'sum')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[3]:
[{'type': 'Feature', 'properties': {'sum': 14539.87501166888}},
{'type': 'Feature', 'properties': {'sum': 4149.850504104552}},
{'type': 'Feature', 'properties': {'sum': 66866.70795363998}},
{'type': 'Feature', 'properties': {'sum': 5293.967633164103}},
{'type': 'Feature', 'properties': {'sum': 31920.496896551656}},
{'type': 'Feature', 'properties': {'sum': 9093.449173829771}}]
Output refinements
Before reviewing the results obtained above, we’ll demonstrate a few options that can be used to refine the output of exact_extract.
Output formats
Outputs can be returned in different formats, e.g. a pandas dataframe:
[4]:
exact_extract(pop_count, concelhos, 'sum', output='pandas')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/3454513098.py", line 1, in <module>
exact_extract(pop_count, concelhos, 'sum', output='pandas')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[4]:
| sum | |
|---|---|
| 0 | 14539.875012 |
| 1 | 4149.850504 |
| 2 | 66866.707954 |
| 3 | 5293.967633 |
| 4 | 31920.496897 |
| 5 | 9093.449174 |
Including source columns
In many cases, it is useful to include some information from the source dataset. Columns to copy from the source dataset can be specified with include_cols or include_geom:
[5]:
exact_extract(pop_count, concelhos, 'sum', include_cols='name', output='pandas')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/1229484743.py", line 1, in <module>
exact_extract(pop_count, concelhos, 'sum', include_cols='name', output='pandas')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[5]:
| name | sum | |
|---|---|---|
| 0 | Lagoa | 14539.875012 |
| 1 | Nordeste | 4149.850504 |
| 2 | Ponta Delgada | 66866.707954 |
| 3 | Povoação | 5293.967633 |
| 4 | Ribeira Grande | 31920.496897 |
| 5 | Vila Franca do Campo | 9093.449174 |
Multiple statistics
Multiple statistics can be calculated by providing a list:
[6]:
exact_extract(pop_count, concelhos, ['sum', 'max', 'max_center_x', 'max_center_y'], include_cols='name', output='pandas')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/1557453004.py", line 1, in <module>
exact_extract(pop_count, concelhos, ['sum', 'max', 'max_center_x', 'max_center_y'], include_cols='name', output='pandas')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[6]:
| name | sum | max | max_center_x | max_center_y | |
|---|---|---|---|---|---|
| 0 | Lagoa | 14539.875012 | 2523.639404 | -25.579167 | 37.745833 |
| 1 | Nordeste | 4149.850504 | 414.669891 | -25.145833 | 37.829167 |
| 2 | Ponta Delgada | 66866.707954 | 3102.277100 | -25.654167 | 37.745833 |
| 3 | Povoação | 5293.967633 | 544.421692 | -25.245833 | 37.745833 |
| 4 | Ribeira Grande | 31920.496897 | 4133.354492 | -25.579167 | 37.812500 |
| 5 | Vila Franca do Campo | 9093.449174 | 1334.649658 | -25.437500 | 37.712500 |
We can also specify a column name that is different from the stat:
[7]:
exact_extract(pop_count, concelhos, 'total_pop=sum', include_cols='name', output='pandas')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/1298948710.py", line 1, in <module>
exact_extract(pop_count, concelhos, 'total_pop=sum', include_cols='name', output='pandas')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[7]:
| name | total_pop | |
|---|---|---|
| 0 | Lagoa | 14539.875012 |
| 1 | Nordeste | 4149.850504 |
| 2 | Ponta Delgada | 66866.707954 |
| 3 | Povoação | 5293.967633 |
| 4 | Ribeira Grande | 31920.496897 |
| 5 | Vila Franca do Campo | 9093.449174 |
Interpreting the results
We might reasonably expect the total population to equal the value of 145,603 we previously obtained by summing the entire raster, but it doesn’t. In fact, 9% of the population is unaccounted for in the concelho totals.
[8]:
_['total_pop'].sum()
[8]:
np.float64(131864.34717295895)
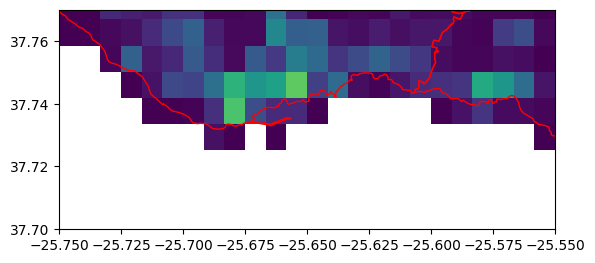
The cause of the discrepancy can be seen by looking closely at the densely populated Ponta Delgada region on the southern coast. Many of the cells containing population are only partially covered by the concelho boundaries, so some of the total population calculated from the full raster is missing from the totals.
[9]:
fig, ax = pyplot.subplots()
ax.set_xlim([-25.75, -25.55])
ax.set_ylim([37.70, 37.77])
with rasterio.open(pop_count) as r:
rasterio.plot.show(r, ax=ax)
gpd.read_file(concelhos) \
.plot(ax=ax, facecolor='none', edgecolor='red')
[9]:
<Axes: >
Calculating population from population density
It turns out that we need a somewhat more complex solution to get accurate population counts when our polygons follow coastlines. Instead of using the population count raster, we bring in the population density raster, which provides the number of persons per square kilometer of land area in each pixel.
[10]:
pop_density = 'sao_miguel/gpw_v411_2020_density_2020.tif'
When calculating a sum, exactextract multiples the value of each pixel by the fraction of the pixel that is covered by the polygon. To calculate the total population from a population density raster, we would need the product of the population density, the fraction of the pixel that is covered, and the pixel area. We could compute this by creating a raster of pixel areas, and using the weighted_sum operation to calculate the product of these three values.
A simpler alternative is to provide an argument to the sum operation, stating that we want pixel values to be multiplied by the area of the pixel that is covered, rather than the fraction of the pixel that is covered.
[11]:
exact_extract(pop_density, concelhos, 'total_pop=sum(coverage_weight=area_spherical_km2)', include_cols='name', output='pandas')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/94884690.py", line 1, in <module>
exact_extract(pop_density, concelhos, 'total_pop=sum(coverage_weight=area_spherical_km2)', include_cols='name', output='pandas')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[11]:
| name | total_pop | |
|---|---|---|
| 0 | Lagoa | 15788.098349 |
| 1 | Nordeste | 4537.404879 |
| 2 | Ponta Delgada | 71370.694085 |
| 3 | Povoação | 5997.344061 |
| 4 | Ribeira Grande | 36131.403400 |
| 5 | Vila Franca do Campo | 11768.354484 |
The total population is then calculated as:
[12]:
_['total_pop'].sum()
[12]:
np.float64(145593.29925670772)
This much more closely matches the value of 145,603 we obtained by summing the entire raster.
Population-weighted statistics
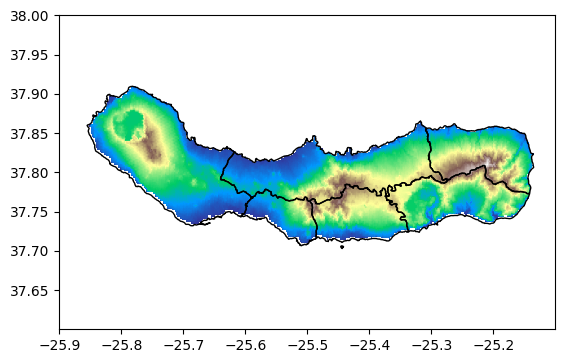
Suppose that we are interested in calculating the average elevation of a residence in each of the six concelhos. Loading the EU-DEM elevation data for the island, we can see that each concelho is at least partly occupied by interior mountains, indicating that the results of a simple mean would be unrepresentative of the primarily coastal population.
[13]:
dem = 'sao_miguel/eu_dem_v11.tif'
fig, ax = pyplot.subplots()
with rasterio.open(dem) as r:
rasterio.plot.show(r, ax=ax, cmap='terrain')
admin = gpd.read_file(concelhos)
admin.plot(ax=ax, facecolor='none', edgecolor='black')
[13]:
<Axes: >
As in the previous section, we avoid working with the population count raster to avoid losing population along the coastline. We can formulate the population-weighted average elevation as in terms of population density and pixel areas as:
where \(x_i\) is the elevation of pixel \(i\), \(c_i\) is the fraction of pixel \(i\) that is covered by a polygon, \(d_i\) is the population density of pixel \(i\), and \(a_i\) is the area of pixel \(i\).
Constant pixel area
If we are working with projected data, or geographic data over a small area such as São Miguel, we can assume all pixel areas to be equivalent, in which case the \(a_i\) components cancel each other out and we are left with the direct usage of population density as a weighting raster:
[14]:
exact_extract(dem, concelhos, ['mean', 'weighted_mean'], weights=pop_density, include_cols='name', output='pandas')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/1577746011.py", line 1, in <module>
exact_extract(dem, concelhos, ['mean', 'weighted_mean'], weights=pop_density, include_cols='name', output='pandas')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/1577746011.py", line 1, in <module>
exact_extract(dem, concelhos, ['mean', 'weighted_mean'], weights=pop_density, include_cols='name', output='pandas')
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 432, in exact_extract
weights = prep_raster(weights, name_root="weight")
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[14]:
| name | mean | weighted_mean | |
|---|---|---|---|
| 0 | Lagoa | 233.720475 | 76.874733 |
| 1 | Nordeste | 453.808604 | 192.470741 |
| 2 | Ponta Delgada | 274.439509 | 97.739504 |
| 3 | Povoação | 375.483205 | 170.464390 |
| 4 | Ribeira Grande | 312.035054 | 74.849762 |
| 5 | Vila Franca do Campo | 418.779671 | 92.205743 |
Non-constant pixel area
What if pixel areas do vary across the region of our analysis? In this case, we can again use the coverage_weight argument to specify that \(c_i\) in the above formula should be the covered area, not the covered fraction. In this case, we can see that considering variations in pixel area does not significantly affect the result.
[15]:
exact_extract(dem, concelhos,
['mean', 'simple_weighted_mean=weighted_mean', 'weighted_mean(coverage_weight=area_spherical_m2)'],
weights=pop_density,
include_cols='name',
output='pandas')
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/3217795958.py", line 1, in <module>
exact_extract(dem, concelhos,
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 431, in exact_extract
rast = prep_raster(rast)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
A module that was compiled using NumPy 1.x cannot be run in
NumPy 2.3.4 as it may crash. To support both 1.x and 2.x
versions of NumPy, modules must be compiled with NumPy 2.0.
Some module may need to rebuild instead e.g. with 'pybind11>=2.12'.
If you are a user of the module, the easiest solution will be to
downgrade to 'numpy<2' or try to upgrade the affected module.
We expect that some modules will need time to support NumPy 2.
Traceback (most recent call last): File "<frozen runpy>", line 198, in _run_module_as_main
File "<frozen runpy>", line 88, in _run_code
File "/usr/local/lib/python3.11/dist-packages/ipykernel_launcher.py", line 18, in <module>
app.launch_new_instance()
File "/usr/local/lib/python3.11/dist-packages/traitlets/config/application.py", line 1075, in launch_instance
app.start()
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelapp.py", line 758, in start
self.io_loop.start()
File "/usr/local/lib/python3.11/dist-packages/tornado/platform/asyncio.py", line 211, in start
self.asyncio_loop.run_forever()
File "/usr/lib/python3.11/asyncio/base_events.py", line 607, in run_forever
self._run_once()
File "/usr/lib/python3.11/asyncio/base_events.py", line 1922, in _run_once
handle._run()
File "/usr/lib/python3.11/asyncio/events.py", line 80, in _run
self._context.run(self._callback, *self._args)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 614, in shell_main
await self.dispatch_shell(msg, subshell_id=subshell_id)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 471, in dispatch_shell
await result
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 366, in execute_request
await super().execute_request(stream, ident, parent)
File "/usr/local/lib/python3.11/dist-packages/ipykernel/kernelbase.py", line 827, in execute_request
reply_content = await reply_content
File "/usr/local/lib/python3.11/dist-packages/ipykernel/ipkernel.py", line 458, in do_execute
res = shell.run_cell(
File "/usr/local/lib/python3.11/dist-packages/ipykernel/zmqshell.py", line 663, in run_cell
return super().run_cell(*args, **kwargs)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3116, in run_cell
result = self._run_cell(
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3171, in _run_cell
result = runner(coro)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/async_helpers.py", line 128, in _pseudo_sync_runner
coro.send(None)
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3394, in run_cell_async
has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3639, in run_ast_nodes
if await self.run_code(code, result, async_=asy):
File "/usr/local/lib/python3.11/dist-packages/IPython/core/interactiveshell.py", line 3699, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "/tmp/ipykernel_758/3217795958.py", line 1, in <module>
exact_extract(dem, concelhos,
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 432, in exact_extract
weights = prep_raster(weights, name_root="weight")
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 140, in prep_raster
sources = loader(rast, name_root)
File "/usr/local/lib/python3.11/dist-packages/exactextract/exact_extract.py", line 44, in prep_raster_gdal
from osgeo import gdal, gdal_array # noqa: F401
File "/usr/lib/python3/dist-packages/osgeo/gdal_array.py", line 13, in <module>
from . import _gdal_array
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
AttributeError: _ARRAY_API not found
[15]:
| name | mean | simple_weighted_mean | weighted_mean | |
|---|---|---|---|---|
| 0 | Lagoa | 233.720475 | 76.874733 | 76.873205 |
| 1 | Nordeste | 453.808604 | 192.470741 | 192.475210 |
| 2 | Ponta Delgada | 274.439509 | 97.739504 | 97.718672 |
| 3 | Povoação | 375.483205 | 170.464390 | 170.454343 |
| 4 | Ribeira Grande | 312.035054 | 74.849762 | 74.849524 |
| 5 | Vila Franca do Campo | 418.779671 | 92.205743 | 92.201693 |